Memory Layout of Multi-dimensional Arrays
Multidimensional arrays are stored as contiguous data in memory. There’s freedom of choice in how to arrange the array elements in this memory segment. Consider the case of a two-dimensional array, containing rows and columns:
-
One possible way to store this array as a consecutive sequence of values is to store the rows after each other, and another equally valid approach is to store the columns one after another.
-
The former is called row-major format and the latter is column-major format.
| Memory Layout | Format |
|---|---|
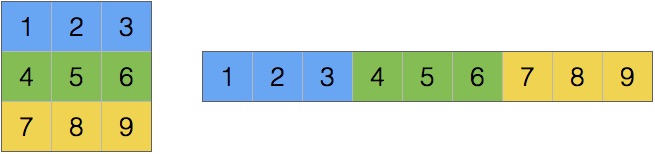 |
row-major |
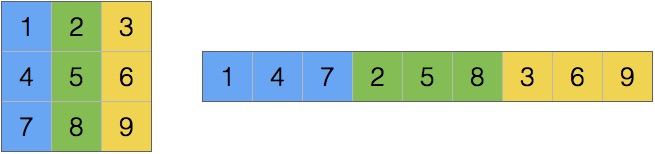 |
column-major |
-
Whether to use row-major or column-major is a matter of conventions, and row-major format is used, for example, in the C programming language, whereas Fortran uses the column-major format.
-
A NumPy array can be specified to be stored in row-major format, using the keyword argument
order='C', and the column-major format, using the keyword argumentorder='F', when the array is created or reshaped. -
The default format is row-major.
-
The
'C'or'F'ordering of NumPy array is particularly relevant when NumPy arrays are used in interfaces with software written in C and Fortran, which is often required when working with numerical computing with Python. -
Row-major and column-major ordering are special cases of strategies for mapping the index used to address an element, to the offset for the element in the array’s memory segment.
-
In general, the NumPy array attribute
ndarray.stridesdefines exactly how this mapping is done. -
The strides attribute is a tuple of the same length as the number of axes (dimensions) of the array. Each value in strides is the factor by which the index for the corresponding axis is multiplied when calculating the memory offset (in bytes) for a given index expression.
Let’s see how this looks:
import numpy as np
arrc = np.array([[1, 2, 3], [11, 12, 13], [21, 22, 23]],
dtype='uint8', order='C')
arrf = np.array([[1, 2, 3], [11, 12, 13], [21, 22, 23]],
dtype='uint8', order='F')
arrc
arrc.itemsize # Each item uses 1 byte because the data type is uint8
The strides attribute of this array is therefore (1x3, 1x1) = (3, 1), because each increment of m=3 in A[n, m] increases the memory offset with one item or 1 byte. Likewise, each increment of n increases the memory offset with three items or 3 bytes (because the second dimension of the array has lenght 3)
arrc.strides
' '.join(str(x) for x in np.nditer(arrc))
arrc.flags
In "C" order, elements of rows are contiguous, as expected. Let’s try Fortran layout now:
arrf
arrf.strides
' '.join(str(x) for x in np.nditer(arrf))
arrf.flags
-
Using strides to describe the mapping of array index to array memory offset is clever because it can be used to describe different mapping strategies, and many common operations on arrays, such as for example the transpose, can be implemented by simply changing the strides attribute, which can eliminate the need for moving data around in the memory.
-
Operations that only require changing the strides attribute result in new ndarray objects that refer to the same data as the original array. Such arrays are called views.
-
For efficiency, NumPy strives to create views rather than copies when applying operations on arrays. This is generally a good thing, but it is important to be aware of that some array operations result in views rather than new independent arrays, because modifying their data also modifies the data of the original array.
%load_ext watermark
%watermark --iversion -g -m -v -u -d